#Algorithm

This article is going to explain the Best Time to Buy and Sell Stock series on LeetCode. The following is the relative link:

Best Time to Buy and Sell Stock

Say you have an array for which the ith element is the price of a given stock on day i.

If you were only permitted to complete at most one transaction (ie, buy one and sell one share of the stock), design an algorithm to find the maximum profit.

Example 1:

Input: [7, 1, 5, 3, 6, 4]
Output: 5
max. difference = 6-1 = 5 (not 7-1 = 6, as selling price needs to be larger than buying price)

Example 2:

Input: [7, 6, 4, 3, 1]
Output: 0
In this case, no transaction is done, i.e. max profit = 0.

Because we are only permitted to complete at most one transaction, the problem becomes find the largest gap among the array max(xi-xj), i > j.

public int maxProfit(int[] prices){
  int currMax = 0;
  int totalMax = 0;
  for(int i = 1; i < prices.length; i++){
      currMax = Math.max(0, currMax+prices[i]-prices[i-1]);
      totalMax = Math.max(totalMax, currMax);
  }
  return totalMax;
}

Best Time to Buy and Sell Stock II

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times). However, you may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

Because it allows multiple transaction as we like, so, when the gap between each time is greater than zero, we should do a transaction. And the logic is slightly simple:

public int maxProfit(int[] prices) {
    int max = 0;
    for(int i = 1; i < prices.length; i++){
        int tmp = prices[i]-prices[i-1];
        if(tmp > 0){
            max += tmp; 
        }
    }
    return max;
}

Best Time to Buy and Sell Stock with Cooldown

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions:

You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).
After you sell your stock, you cannot buy stock on next day. (ie, cooldown 1 day)

Example:

1
2
3

prices = [1, 2, 3, 0, 2]
maxProfit = 3
transactions = [buy, sell, cooldown, buy, sell]

This problem can be solved by State Machine thinking. And I learned this problem the leetcode Discussion

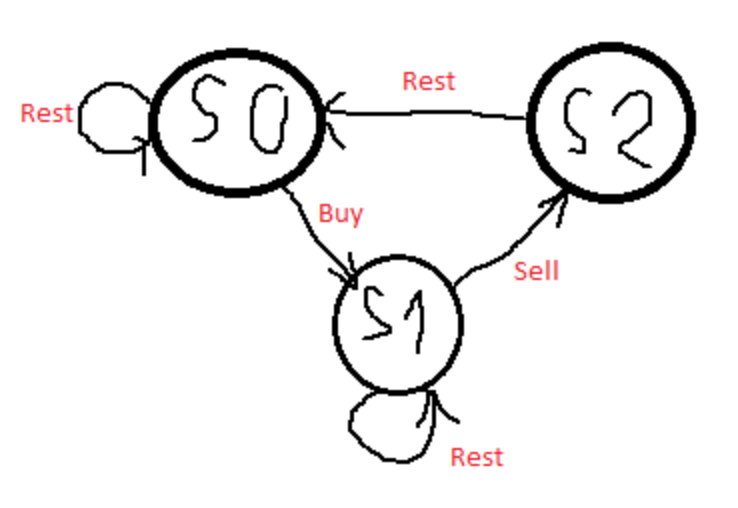state We can know that s0 can be only obtained by rest at itself or rest from s2, s1 and be only obtained by rest at itself or buy from s0, s2 can be obtained only by sell product from s1.

So we will have:

1
2
3

s0[i] = Math.max(s0[i-1],s2[i-1]);
s1[i] = Math.max(s1[i-1],s0[i-1]-prices[i]);
s2[i] = s1[i-1]+prices[i];

We know that s1 will never be the largest state, because it buy(cost money) and remain same must be smaller than s0. So, the maximum state must among s0 or s2.

public int maxProfit(int[] prices) {
    if(prices.length == 0){
        return 0;
    }
    int s0 = 0, s0prev = 0;
    int s1 = 0, s1prev=-prices[0];
    int s2 = 0, s2prev=Integer.MIN_VALUE;
    for(int p : prices){
        s0 = Math.max(s0prev,s2prev);
        s1 = Math.max(s1prev,s0prev-p);
        s2 = Math.max(s2prev,s1prev+p);
        s0prev=s0;
        s1prev=s1;
        s2prev=s2;
    }
    return Math.max(s0,s2);
}

Best Time to Buy and Sell Stock with Transaction Fee

Your are given an array of integers prices, for which the i-th element is the price of a given stock on day i; and a non-negative integer fee representing a transaction fee.

You may complete as many transactions as you like, but you need to pay the transaction fee for each transaction. You may not buy more than 1 share of a stock at a time (ie. you must sell the stock share before you buy again.)

Return the maximum profit you can make.

Example 1:

Input: prices = [1, 3, 2, 8, 4, 9], fee = 2
Output: 8
Explanation: The maximum profit can be achieved by:
Buying at prices[0] = 1Selling at prices[3] = 8Buying at prices[4] = 4Selling at prices[5] = 9The total profit is ((8 - 1) - 2) + ((9 - 4) - 2) = 8.

This problem is similar to the Problem II, the difference if we have more transactions, we may cost more fees which may decrease the total profit. So, when calculating the cash, we need to consider that fee. The following is the code, and I will explain it with comment:

public int maxProfit(int[] prices, int fee) {
    int sell = 0, buy = -prices[0], maxSell = 0;
    for(int i = 1; i < prices.length;i++){
        sell = Math.max(sell, buy+prices[i]-fee);//sell
        buy = Math.max(buy, sell-prices[i]);//buy
        maxSell = Math.max(sell, maxSell);
    }
    return maxSell;
}

Line 4 stands for the current profit we have, hold+prices[i]-fee means the profit we have after do a transaction. Compare this the current cash.

Line 5 stands for the hold money, which means we do a buy a product.

Best Time to Buy and Sell Stock III

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most two transactions.

Note:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

The following code is explained with comment:

public int maxProfit(int[] prices) {
    int firstBuy = Integer.MIN_VALUE;
    int afterFirstSell = 0;
    int afterSecondBuy = Integer.MIN_VALUE;
    int afterSecondSell = 0;
    for(int p:prices){
        firstBuy = Math.max(firstBuy, -p); //FirstBuy should be as lower as possible
        afterFirstSell = Math.max(afterFirstSell, p+firstBuy); //Maximize the first sell profit
        afterSecondBuy = Math.max(afterSecondBuy,afterFirstSell-p); //Let Second buy still ensure max profit
        afterSecondSell = Math.max(afterSecondSell, p+afterSecondBuy); //Maximize the second sell profit
        }
    return afterSecondSell;
}

Best Time to Buy and Sell Stock IV

Say you have an array for which the ith element is the price of a given stock on day i.

Design an algorithm to find the maximum profit. You may complete at most k transactions.

Note:
You may not engage in multiple transactions at the same time (ie, you must sell the stock before you buy again).

The idea is almost same as the previous one, but we need to extend it to a two dimension int array rather than store in four variables. And another thing we need to notice is if k >= n/2, the problem will be the same as II problem, because the limit of transactions will not be a constraint for us. And the code is as follow:

public int maxProfit(int k, int[] prices) {
    int n = prices.length;
    if(k == 0){
        return 0;
    }
    if(k >= n /2){
        int maxPro = 0;
        for (int i = 1; i < n; i++) {
            if (prices[i] > prices[i-1]){
                maxPro += prices[i] - prices[i-1];
            }
        }
        return maxPro;
    }
    int[][] dp = new int[k][2];
    for(int i = 0; i < k; i++){
        dp[i][0] = Integer.MIN_VALUE;
        dp[i][1] = 0;
    }
    for(int p : prices){
        dp[0][0] = Math.max(dp[0][0], -p);
        dp[0][1] = Math.max(dp[0][1], p+dp[0][0]);
        for(int i = 1; i < k; i++){
            dp[i][0] = Math.max(dp[i][0], dp[i-1][1]-p);
            dp[i][1] = Math.max(dp[i][1], dp[i][0]+p);
        }
    }
    return dp[k-1][1];
}

All done with Best Time to Buy and Sell Stock problem. :-) Hope you can have a good understanding of Dynamic Programming in this problem. :D Any questions, please leave a comment below. :-)

Best Time to Buy and Sell Stock series with Dynamic Programming in Java

Best Time to Buy and Sell Stock

Best Time to Buy and Sell Stock II

Best Time to Buy and Sell Stock with Cooldown

Best Time to Buy and Sell Stock with Transaction Fee

Best Time to Buy and Sell Stock III

Best Time to Buy and Sell Stock IV

Comments: